Coding Warmup 4

Make a classification model and run evaluations.

Part A

We are going to use a toy dataset called bivariate. There is a training, testing, and validation dataset provided.

library(tidyverse)
library(tidymodels)
theme_set(theme_bw())

data(bivariate)

ggplot(bivariate_train, aes(x=A, y=B, color=Class)) +
  geom_point(alpha=.3)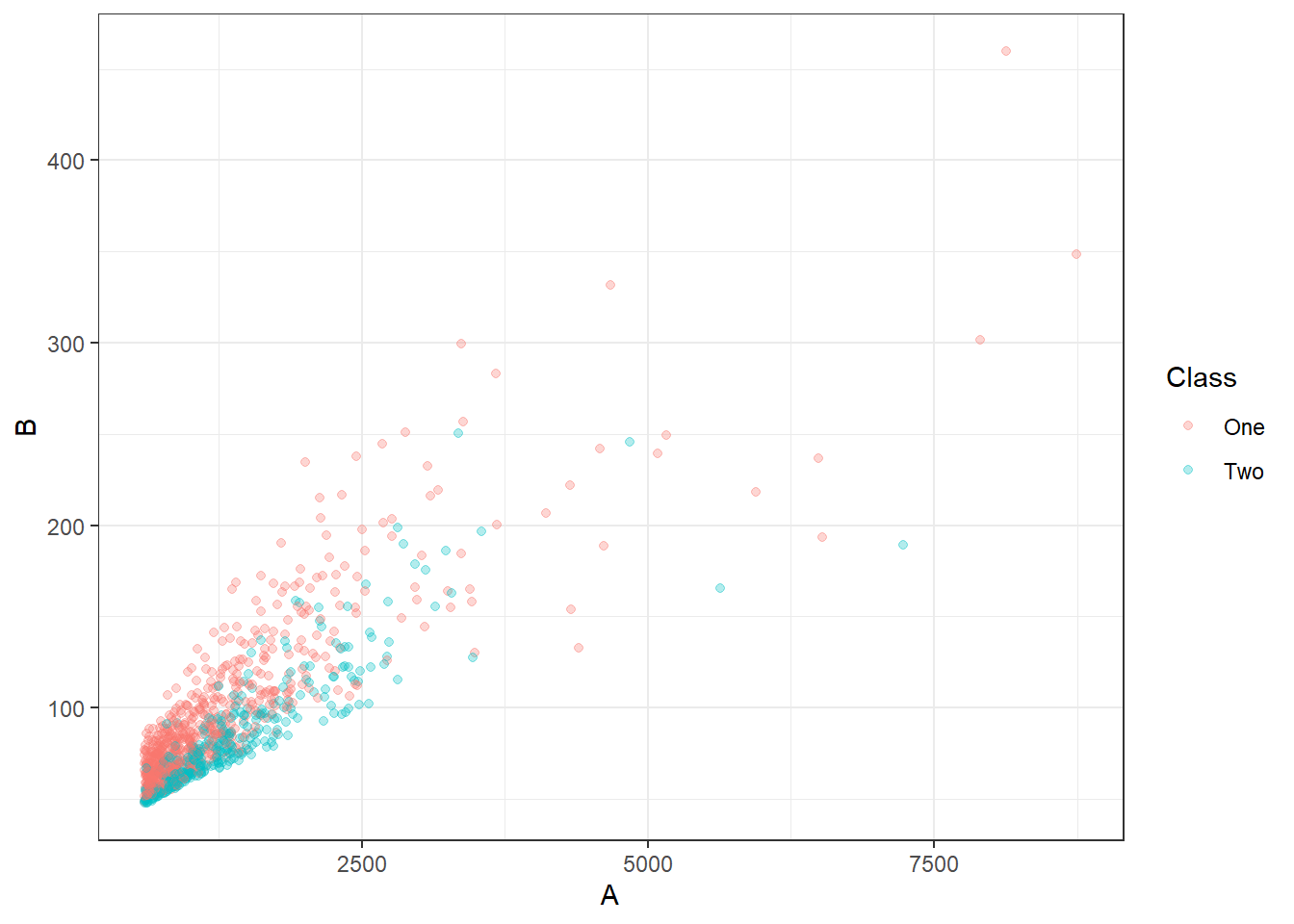

Use logistic_reg and glm to make a classification model of Class ~ A * B. Then use tidy and glance to see some summary information on our model. Anything stand out to you?

log_model <- logistic_reg() %>%
  set_engine('glm') %>%
  set_mode('classification') %>%
  fit(Class ~ A*B,
      data = bivariate_train)

log_model %>% tidy()

## # A tibble: 4 × 5
##   term          estimate  std.error statistic  p.value
##   <chr>            <dbl>      <dbl>     <dbl>    <dbl>
## 1 (Intercept)  0.115     0.404          0.284 7.76e- 1
## 2 A            0.00433   0.000434       9.97  2.01e-23
## 3 B           -0.0553    0.00633       -8.74  2.32e-18
## 4 A:B         -0.0000101 0.00000222    -4.56  5.04e- 6

log_model %>% broom::glance()

## # A tibble: 1 × 8
##   null.deviance df.null logLik   AIC   BIC deviance df.residual  nobs
##           <dbl>   <int>  <dbl> <dbl> <dbl>    <dbl>       <int> <int>
## 1         1329.    1008  -549. 1106. 1126.    1098.        1005  1009

Part B

Use augment to get predictions. Look at the predictions.

test_preds <- log_model %>% augment(bivariate_test)

test_preds

## # A tibble: 710 × 6
##    .pred_class .pred_One .pred_Two     A     B Class
##    <fct>           <dbl>     <dbl> <dbl> <dbl> <fct>
##  1 One           0.730      0.270   742.  68.8 One  
##  2 Two           0.491      0.509   709.  50.4 Two  
##  3 One           0.805      0.195  1006.  89.9 One  
##  4 Two           0.431      0.569  1983. 112.  Two  
##  5 Two           0.169      0.831  1698.  81.0 Two  
##  6 One           0.900      0.0996  948.  98.9 One  
##  7 One           0.521      0.479   751.  54.8 One  
##  8 Two           0.347      0.653  1254.  72.2 Two  
##  9 Two           0.00568    0.994  4243. 136.  One  
## 10 One           0.910      0.0898  713.  88.2 One  
## # ℹ 700 more rows

Part C

Visually inspect the predictions using the code below

# log_model, your parnsip model
# bivariate_train / bivariate_val, data from bivariate

# to plot the countour we need to create a grid of points and get the model prediction at each point
x_grid <-
  expand.grid(A = seq(min(bivariate_train$A), max(bivariate_train$A), length.out = 100),
              B = seq(min(bivariate_train$B), max(bivariate_train$B), length.out = 100))
x_grid_preds <- log_model %>% augment(x_grid)

# plot predictions from grid as countour and validation data on plot
ggplot(x_grid_preds, aes(x = A, y = B)) + 
  geom_contour(aes(z = .pred_One), breaks = .5, col = "black") + 
  geom_point(data = bivariate_val, aes(col = Class), alpha = 0.3)

# log_model, your parnsip model
# bivariate_train / bivariate_val, data from bivariate

# to plot the countour we need to create a grid of points and get the model prediction at each point
x_grid <-
  expand.grid(A = seq(min(bivariate_train$A), max(bivariate_train$A), length.out = 100),
              B = seq(min(bivariate_train$B), max(bivariate_train$B), length.out = 100))
x_grid_preds <- log_model %>% augment(x_grid)

# plot predictions from grid as countour and validation data on plot
ggplot(x_grid_preds, aes(x = A, y = B)) + 
  geom_contour(aes(z = .pred_One), breaks = .5, col = "black") + 
  geom_point(data = bivariate_val, aes(col = Class), alpha = 0.3)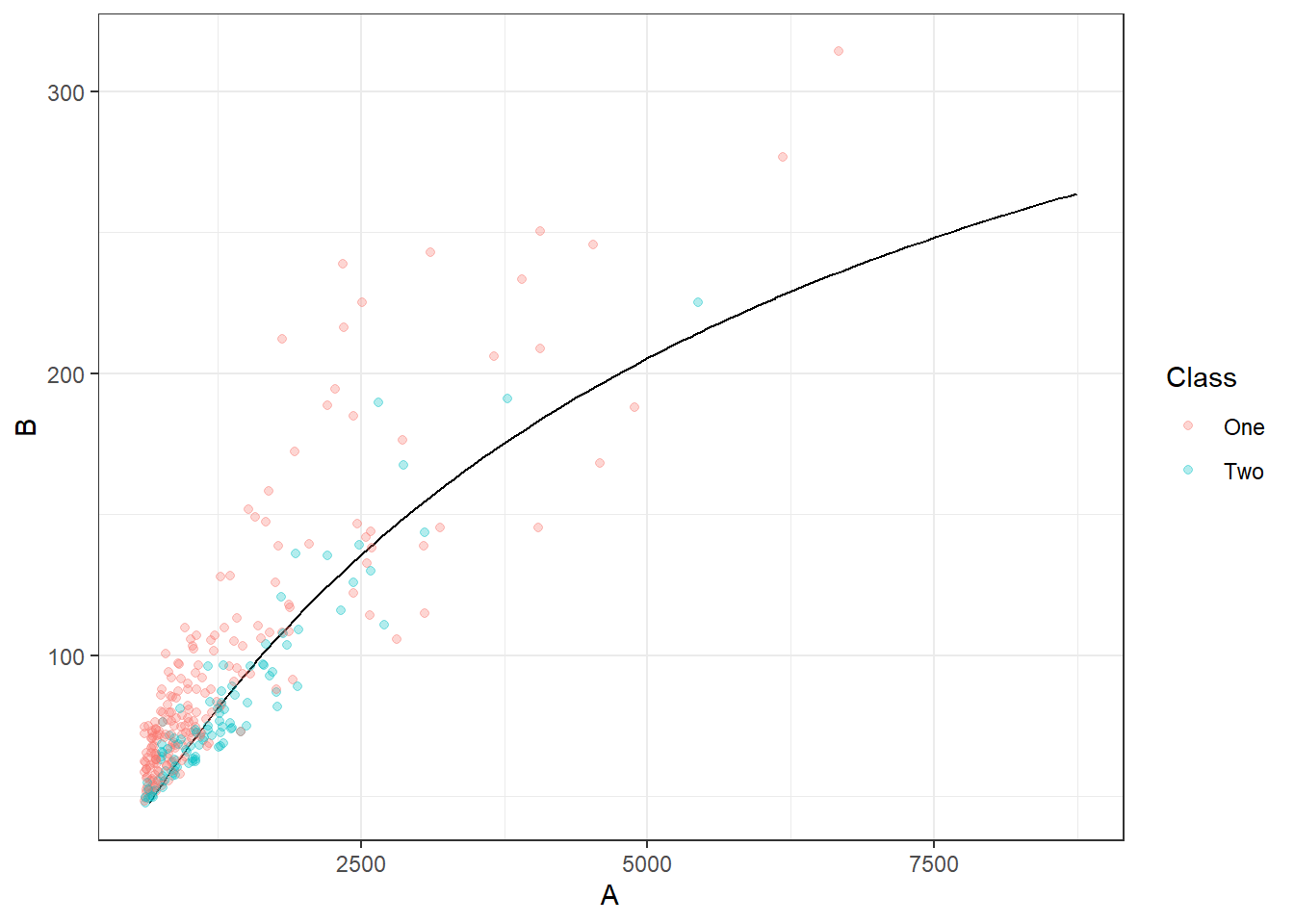

Part D

Evaluate your model using the following functions (which dataset(s) should you use to do this train, test, or validation). See if you can provide a basic interpretation of the measures.

roc_auc
accuracy
roc_curve and autoplot
f_meas

val_preds <- log_model %>% augment(bivariate_val)

val_preds %>% roc_auc(Class,
                      .pred_One)

## # A tibble: 1 × 3
##   .metric .estimator .estimate
##   <chr>   <chr>          <dbl>
## 1 roc_auc binary         0.790

val_preds %>% accuracy(Class,
                      .pred_class)

## # A tibble: 1 × 3
##   .metric  .estimator .estimate
##   <chr>    <chr>          <dbl>
## 1 accuracy binary          0.76

roc_curve(val_preds,
        Class,
        .pred_One) %>%
  autoplot()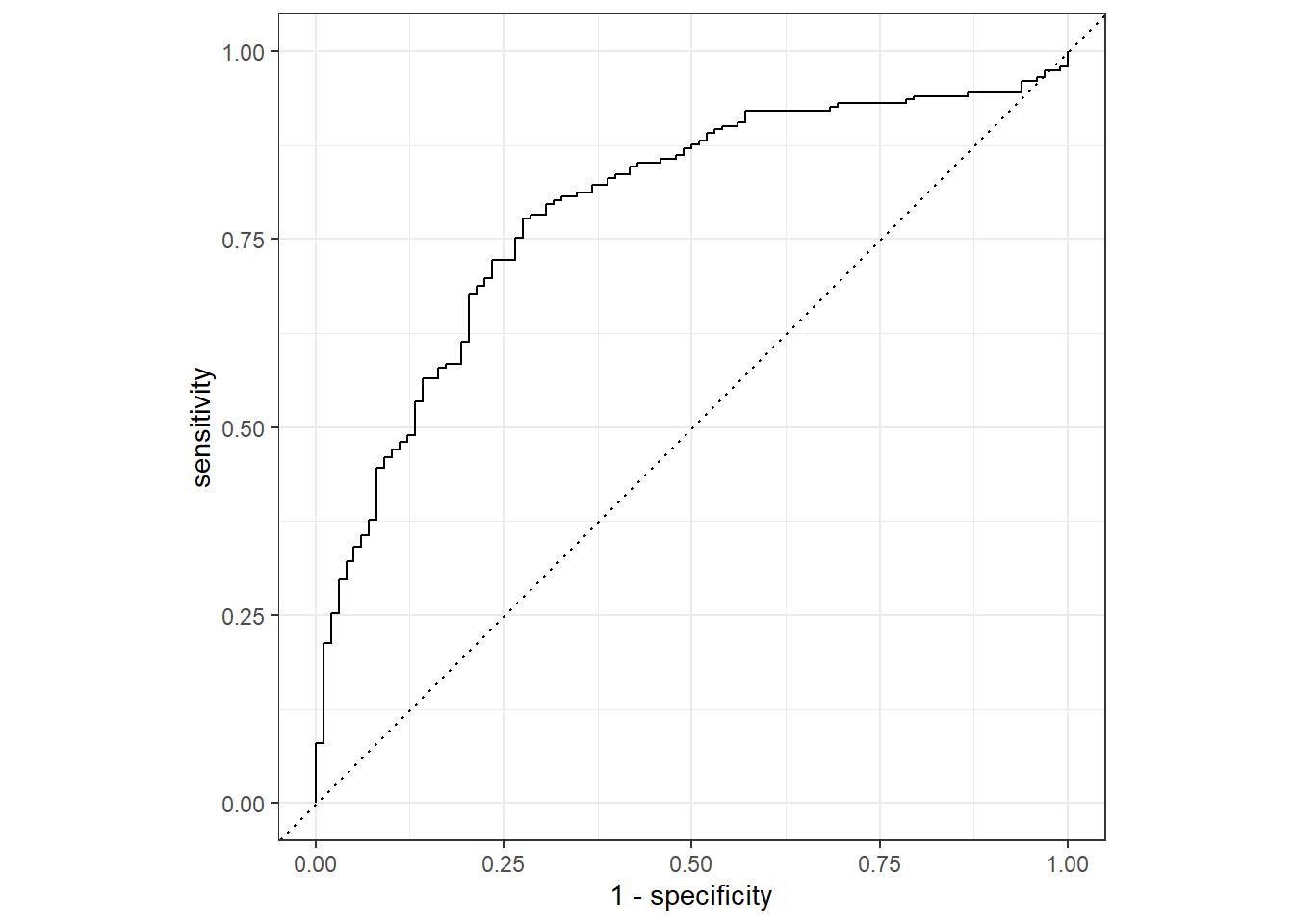

f_meas(val_preds,
        Class,
        .pred_class)

## # A tibble: 1 × 3
##   .metric .estimator .estimate
##   <chr>   <chr>          <dbl>
## 1 f_meas  binary         0.827

Part E

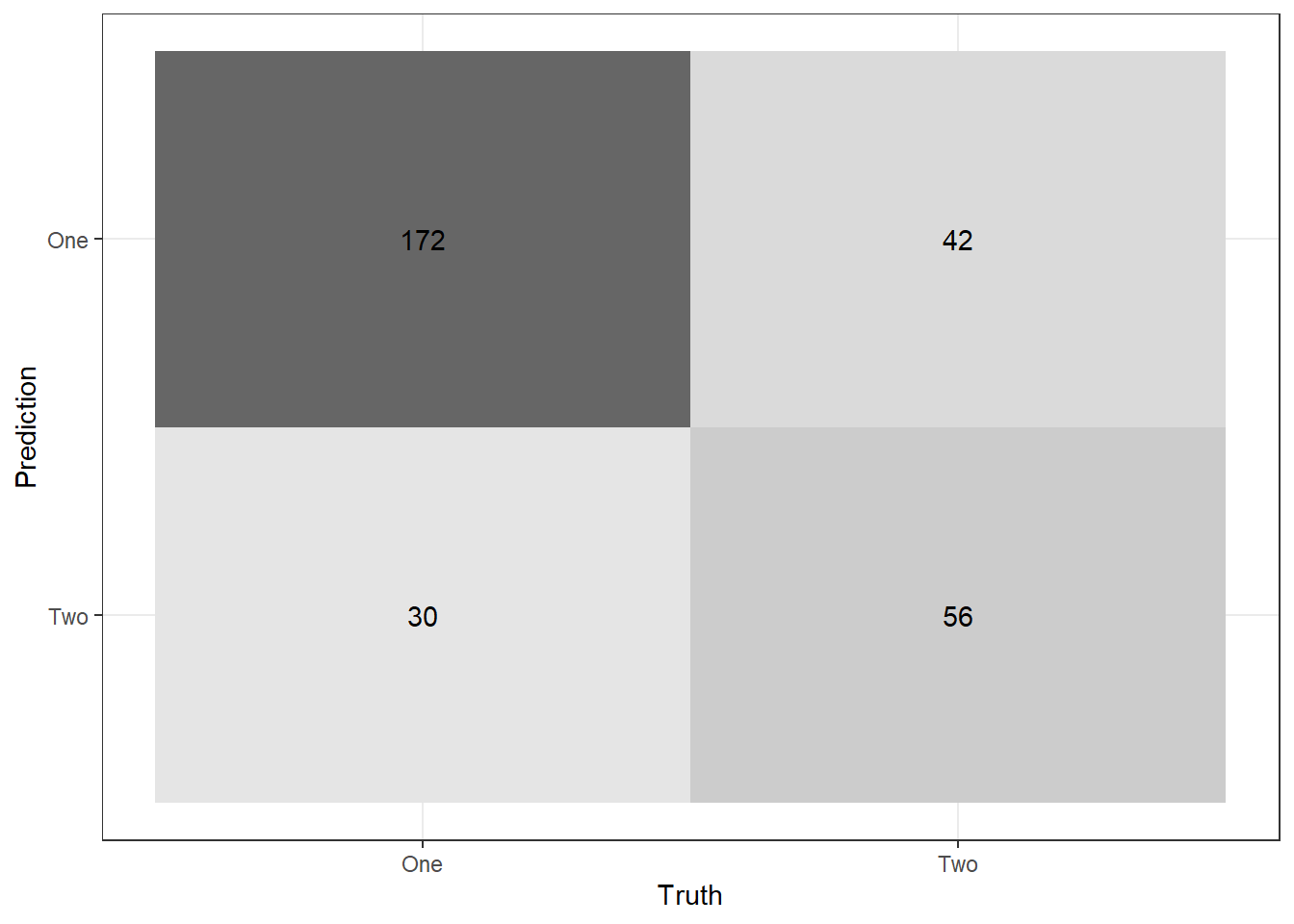
Recall Table 8.4 from the textbook. If necessary, class one can be positive and class two can be negative. Using the output from conf_mat, visually verify you know how to calculate the following:

True Positive Rate (TPR), Sensitivity, or Recall
True Negative Rate (TNR) or Specificity
False Positive Rate, Type I error
False Negative Rate (FNR), Type II error
Positive Predictive Value (PPV) or Precision

val_preds %>% conf_mat(truth = Class,
                      estimate = .pred_class) %>%
  autoplot("heatmap")